今天看了大神写的关于贝塞尔曲线的博客,就写下了关于手指轨迹的一篇博客,
一、什么是贝塞尔曲线
贝塞尔曲线(Bézier curve),又称贝兹曲线或贝济埃曲线,是应用于二维图形应用程序的数学曲线。一般的矢量图形软件通过它来精确画出曲线,贝兹曲线由线段与节点组成,节点是可拖动的支点,线段像可伸缩的皮筋,我们在绘图工具上看到的钢笔工具就是来做这种矢量曲线的。贝塞尔曲线是计算机图形学中相当重要的参数曲线,在一些比较成熟的位图软件中也有贝塞尔曲线工具,如PhotoShop等。
二、贝塞尔曲线公式

三、手指轨迹原理
因为这个我们用的是自定义控件,所以我们创建一个finger的类集成View,重写onDraw onTouchEvent这个两个方法
public finger(Context context, @Nullable AttributeSet attrs)需要这个构造方法

其实手指轨迹的原理也很简单,就是通过onTouchEvent来获取道手指的位置,来绘制path路径即可。
四、分析代码
这里我先写出全部的代码,后面我再来一一分析代码的作用:
全部代码:
package com.campus.shopping.drawtext;
import android.content.Context;
import android.graphics.Canvas;
import android.graphics.Color;
import android.graphics.Paint;
import android.graphics.Path;
import android.support.annotation.Nullable;
import android.util.AttributeSet;
import android.view.MotionEvent;
import android.view.View;
/**
* Created by sang on 2018/6/24.
*/
public class MyView extends View {
private Path mPath = new Path();
private float mPreX,mPreY;
public MyView(Context context, @Nullable AttributeSet attrs) {
super(context, attrs);
}
@Override
public boolean onTouchEvent(MotionEvent event) {
switch (event.getAction()) {
case MotionEvent.ACTION_DOWN: {
mPath.moveTo(event.getX(), event.getY());
mPreX = event.getX();
mPreY = event.getY();
return true;
}
case MotionEvent.ACTION_MOVE:
float endX = (mPreX+event.getX())/2;
float endY = (mPreY+event.getY())/2;
mPath.quadTo(mPreX,mPreY,endX,endY);
mPreX = event.getX();
mPreY = event.getY();
invalidate();
break;
default:
break;
}
return super.onTouchEvent(event);
}
public void reset(){
mPath.reset();
invalidate();
}
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
Paint paint = new Paint();
paint.setColor(Color.WHITE);
paint.setStyle(Paint.Style.STROKE);
canvas.drawPath(mPath, paint);
}
}onTouchEvent方法:
public boolean onTouchEvent(MotionEvent event) {
switch (event.getAction()) {
case MotionEvent.ACTION_DOWN: {
mPath.moveTo(event.getX(), event.getY());
mPreX = event.getX();
mPreY = event.getY();
return true;
}
case MotionEvent.ACTION_MOVE:
float endX = (mPreX+event.getX())/2;
float endY = (mPreY+event.getY())/2;
mPath.quadTo(mPreX,mPreY,endX,endY);
mPreX = event.getX();
mPreY = event.getY();
invalidate();
break;
default:
break;
}
return super.onTouchEvent(event);
}当手指按下触发了ACTION_DOWN时,这里我通过moveTo的方法绘制了第一个点,这个必须使用moveTo,因为如果不使用这个这个点将会在(0,0)开始,最后我们回去到xy点作为控制点,最后使用返回 真的方式让ACTION_MOVE,ACTION_UP事件往这个控件继续传递事件。
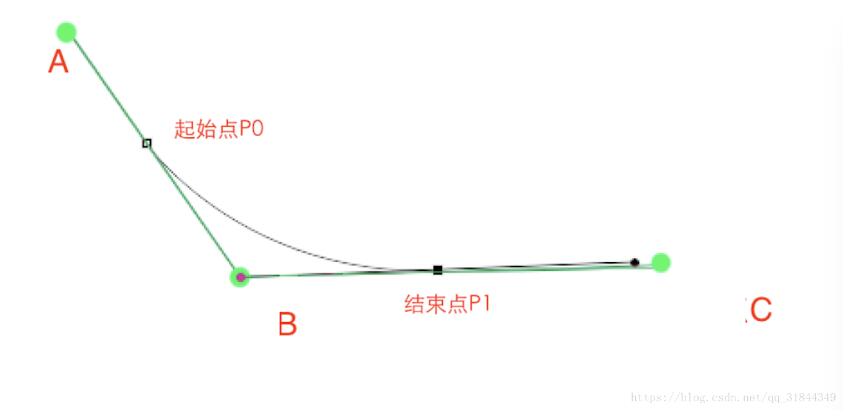
再来看当触发ACTION_MOVE时,因为贝塞尔曲线是由线段构成的,结束点时在线段的中间的位置,所以这里的计算方法是(起点+最后的点)/2就可以得到中间的点.
使用方式:
<com.campus.shopping.drawtext.finger
android:id="@+id/viewmy"
android:layout_width="fill_parent"
android:layout_height="fill_parent" />
以上就是本文的全部内容,希望对大家的学习有所帮助,也希望大家多多支持得得之家。
